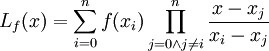czwartek, 31 marca 2016

Programy służące do różnego rodzaju obliczeń:

Microsoft Excel (pełna nazwa Microsoft Office Excel) – arkusz kalkulacyjny produkowany przez firmę Microsoft dla systemów Windows i MacOS. Pierwsza wersja programu przeznaczona dla Windows trafiła na rynek w roku 1987 i stała się przebojem. Postępujący sukces rynkowy programu sprawił, że w roku 1993 programy pakietu Microsoft Office zostały przeprojektowane tak, by przypominać wyglądem arkusz Excel. Od wersji 5 wydanej w 1993 program zawiera wbudowany język Visual Basic. Od wersji 4.0 dostępny w wersji polskiej[1].

Pocket Excel to mobilna wersja popularnego arkusza kalkulacyjnego obecnego w systemach z rodziny Windows Mobile. Doskonale nadaje się do podstawowych operacji na liczbach gdy nie mamy dostępu do biurkowej wersji Microsoft Excela. Jest on po części kompatybilny z wersją programu zawartego w pakiecie Microsoft Office dla komputerów PC.

Zastosowanie

Aplikacja jest powszechnie używana w firmach i instytucjach, a także przez użytkowników domowych. Jej główne zastosowanie to dokonywanie obliczeń (np. wydatków) zestawionych w formie tabelarycznej. W tym użyciu mają zastosowanie liczne funkcje matematyczne, finansowe i bazodanowe dostępne w programie. Istotne znaczenie ma też półautomatyczne powielanie tworzonych formuł z zastosowaniem różnych wariantów adresowania (adresowanie względne, adresowanie bezwzględne, adresowanie mieszane). Microsoft Excel służy także do tworzenia wielu typów wykresów, przydatnych między innymi w fizyce, matematyce i ekonomii. Zawiera też system zestawiania raportów z użyciem tzw. tabel przestawnych, wykorzystywany przy wykonywaniu analiz biznesowych.

Mathematica – komercyjny system obliczeń symbolicznych i numerycznych opracowany w 1988 przez Stephena Wolframa. W ciągu przeszło 20 lat istnienia Mathematica stała się bardzo popularna w środowisku naukowców i inżynierów.

Mathematicę charakteryzują wysoka wydajność, szerokie możliwości wizualizacji i prezentacji danych oraz przenośność. Obecnie jest dostępna na większość platform 32- i 64-bitowych.

Komercyjną konkurencją dla pakietu Mathematica jest Maple. Spośród wolnego oprogramowania podobne funkcje oferują programy Maxima oraz Sage.

Cechy i możliwości:

własny język programowania funkcyjnego podobny do języka Lisp, który operuje na listach i posiada bogate możliwości ich przetwarzania
obliczenia na liczbach rzeczywistych, zespolonych i kwaternionach o precyzji definiowanej jako epsilon maszynowy lub duże liczby całkowite
wykonywanie obliczeń równoległych, w tym obliczeń z wykorzystaniem karty graficznej w technologii CUDA
przekształcenia wyrażeń arytmetycznych zawierających wielomiany, wyrażenia trygonometryczne, wykładnicze, logarytmiczne itd.
rozwiązywanie równań i nierówności różnych typów oraz ich układów
logika matematyczna i algebra Boole'a
algebra liniowa – operacje na skalarach, wektorach i macierzach pod postacią list, przekształcenia i rozkłady macierzy, rozwiązywanie układów równań liniowych, znajdowanie wartości i wektorów własnych, potęgowanie macierzy i funkcje macierzowe, tensory, macierze rzadkie
algebra wyższa – wielomiany rzeczywiste i zespolone, wielomiany diofantyczne, ciała liczbowe, liczby i równania Frobeniusa, ciała skończone (Galois)
matematyka dyskretna – kombinatoryka i optymalizacja kombinatoryczna, równania różnicowe i transformata Z, teoria grafów, teoria grup, automaty skończone i komórkowe
teoria liczb – faktoryzacja, kongruencje, równania diofantyczne, analityczne, addytywne i algebraiczne elementy teorii liczb
szeregi, granice i residua – sumy i iloczyny, szeregi potęgowe i ich przekształcenia, rozwiązywanie równań rekurencyjnych, znajdowanie granic i residuów funkcji, przybliżenie Pade, alternatywne funkcje numerycznego obliczania przybliżeń granic, residuów i pochodnych
rachunek różniczkowy i całkowy – różniczkowanie, różniczka zupełna, całkowanie, całki oznaczone, nieoznaczone funkcji jednej i wielu zmiennych, całkowanie po różnych obszarach, teoria pola, rachunek wariacyjny, ciągłe i dyskretne przekształcenia całkowe Fouriera i Laplace'a , numeryczna aproksymacja przekształcenia Fouriera i odwrotnego przekształcenia Fouriera
analityczne rozwiązywanie niektórych typów równań różniczkowych zwyczajnych, cząstkowych i różniczkowo-algebraicznych, zagadnienia brzegowe liniowe i nieliniowe
numeryczne rozwiązywanie równań różniczkowych zwyczajnych (wiele wariantów metod Eulera i Rungego-Kutty), cząstkowych (metoda linii MOL), różniczkowo-algebraicznych (metoda IDA) i równań różniczkowych ze stałym opóźnieniem (metoda kroków), wykrywanie równań sztywnych, rozwiązywanie problemów brzegowych, interfejs graficzny do analizy równań różniczkowych
całkowanie numeryczne – kwadratury Newtona-Cotesa, Gaussa, Lobatto i Clenshawa-Curtissa, metody Monte-Carlo i quasi Monte-Carlo, metody adaptacyjne lokalne i globalne, strategie oscylacyjne, eliminacja osobliwości
optymalizacja statyczna bez ograniczeń – metody Newtona, gradientu sprzężonego, Levenberga-Marquardta, BFGS i Brenta, optymalizacja kroku poszukiwań, stany początkowe i końcowe optymalizacji
optymalizacja statyczna z ograniczeniami – programowanie liniowe ( metoda simplex, metoda punktu wewnętrznego), numeryczna optymalizacja nieliniowa (lokalna – metoda punktu wewnętrznego, globalna – metoda sympleksu Neldera-Meada, ewolucja różnicowa, symulowane wyżarzanie, przeszukiwanie losowe), analityczna optymalizacja nieliniowa (metoda CAD, metoda mnożników Lagrange'a), programowanie całkowitoliczbowe
prawdopodobieństwo, statystyka i analiza danych – obliczanie prawdopodobieństw, zmienne losowe i ich parametry, ponad sto dystrybuant rozkładów dyskretnych i ciągłych, interpolacja i aproksymacja, funkcje sklejane, sploty i korelacje, estymacja i testowanie hipotez, modele statystyczne
zastosowania w innych dziedzinach wiedzy – teoria sterowania, przetwarzanie sygnałów i przekształcenia falkowe, przetwarzania obrazu i dźwięku, analiza giełdowa i finansowa, eksploracja danych (analiza skupień, dopasowanie sekwencji i dopasowanie do wzorca) i text mining
biblioteka funkcji matematycznych: generatory liczb pseudolosowych, funkcje teorii liczb, funkcje teorii grup, wielomiany ortogonalne, funkcje specjalne i uogólnione, całki i funkcje eliptyczne, stałe matematyczne, fizyczne i jednostki miar
grafika – wykresy 2D i 3D funkcji w postaci zwykłej, parametrycznej i uwikłanej w różnych układach współrzędnych, wykresy specjalne, rysowanie grafów, bryły platońskie, specjalistyczne wykresy statystyczne, opis i modyfikacja wykresów, animacje interaktywne
import danych różnego typu i zapisywanie wyników pracy pod różnymi postaciami (HTML, LaTeX, PostScript, PDF, RTF, CDF, XML z MathLink)
narzędzia integracji z innymi systemami poprzez HTTP, SQL, Java, .NET i C
dostęp do dużej internetowej bazy danych matematycznych, naukowych i socjoekonomicznych w serwisie Wolfram Alpha

Derive – program z rodziny CAS (Computer Algebra System), który pozwala na wykonywanie obliczeń symbolicznych i numerycznych z wielu działów matematyki.

Możliwości programu:

Program jest intuicyjny w obsłudze. Jego możliwości to między innymi:

arytmetyka liczb rzeczywistych (również w układach niedziesiątkowych) i zespolonych
operacje na macierzach i rachunek wektorowy
obliczenia symboliczne na wyrażeniach algebraicznych – wykonywanie działań i redukcja wyrazów podobnych, rozkład na czynniki wielomianów, obliczanie pochodnych, całek, granic funkcji, rozwijanie funkcji w szereg potęgowy
rozwiązywanie układów równań i nierówności wielomianowych
wykresy funkcji jednej i dwóch zmiennych
wersja 6.10 dostępna jest w języku polskim

piątek, 13 listopada 2015

Metoda Newtona

Jeśli f ∈ C^2 [a, b] tworzę ciąg typu

Procedura trwa do momentu aż dla zadanej dokładności δ

Kod programu w C++:

#include<iostream>

#include<cmath>

using namespace std;

double fun(double x)

{

return exp(x)*log(x)-x*x;

}

double fun1(double x)

{

return exp(x)*log(x)+exp(x)*(1./x)-2.*x;

}

int main()

{

double a=1.0;

double b=2.0;

double ab=b-a;

double delta=0.001;

double x0=(a+b)/2.;

double x1;

while( fabs(ab) > delta)

{

x1=x0-fun(x0)/fun1(x0);

ab=x1-x0;

x0=x1;

cout<<x1<<endl;

}

return 0;

}

Otrzymujemy w kolejnych krokach miejsc zerowe:1.7398; 1.69657; 1.6946; 1.6946

czwartek, 5 listopada 2015

A oto film stworzony na zajęciach.

poniedziałek, 12 października 2015

Witam na moim blogu.

Będzie on poświęcony metodom numerycznym, a dokładnie wybranym zagadnieniom z tego działu.

Blog ten tworzony jest na potrzeby przedmiotu "Metody numeryczne". Prowadzącym jest profesor Ihor Ohirko (zdjęcie poniżej).

Co to są metody numeryczne?

Metody numeryczne to dziedzina wiedzy zajmująca się problemami obliczeniowymi i konstrukcją algorytmów rozwiązywania zadań matematycznych. Najczęściej, zadania obliczeniowe postawione są w dziedzinie rzeczywistej (lub zespolonej) i dlatego mówimy o zadaniach obliczeniowych matematyki ciągłej (w odróżnieniu od matematyki dyskretnej).

Metody numeryczne wykorzystywane są wówczas, gdy badany problem nie ma w ogóle rozwiązania analitycznego (danego wzorami) lub korzystanie z takich rozwiązań jest uciążliwe ze względu na ich złożoność.

W szczególności dotyczy to:

całkowania;
znajdowania miejsc zerowych wielomianów stopnia większego niż 2 (korzystanie ze wzorów na dokładne wartości pierwiastków równań stopnia 3 i stopnia 4 jest niepraktyczne, dla równań stopnia wyższego niż 4 wzorów już nie ma);
rozwiązywania układów równań liniowych w przypadku większej liczby równań i niewiadomych;
rozwiązywania równań różniczkowych i układów takich równań;
znajdowania wartości i wektorów własnych (zob. równanie własne);
aproksymacji, czyli przybliżaniu nieznanych funkcji (np. pomiarów zjawisk fizycznych).

Niektóre metody numeryczne

Interpolacja liniowa
Interpolacja wielomianowa
FFT
metoda Monte Carlo
metody Newtona-Cotesa
wzór parabol Simpsona
wzór trapezów
metoda równego podziału
Kwadratury Gaussa

Interpolacja liniowa – szczególny przypadek aproksymacji za pomocą funkcji liniowej.

Aproksymacja (łac. approximare – przybliżać) – proces określania rozwiązań przybliżonych na podstawie rozwiązań znanych, które są bliskie rozwiązaniom dokładnym w ściśle sprecyzowanym sensie. Zazwyczaj aproksymuje się byty (np. funkcje) skomplikowane bytami prostszymi. Często stosowana w przypadku szukania rozwiązań dla danych uzyskanych metodami empirycznymi, które mogą być obarczone błędami.

Jeśli x określa wartość z przedziału x0 < x < x1, a y0 = f(x0) i y1 = f(x1) tablicę wartości danej funkcji, oraz h = x1 - x0 odstęp pomiędzy argumentami, wówczas liniową interpolację wartości L(x) funkcji f otrzymuje się jako:

Interpolacja liniowa

Interpolacja wielomianowa, nazywana też interpolacją Lagrange'a, od nazwiska pioniera badań nad interpolacją Josepha Lagrange'a, lub po prostu interpolacją jest metodą numeryczną przybliżania funkcji tzw. wielomianem Lagrange'a stopnia n przyjmującym w n+1 punktach, zwanych węzłami interpolacji, wartości takie same jak przybliżana funkcja.

Interpolacja jest często stosowana w naukach doświadczalnych, gdzie dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności między wielkościami.

Zgodnie z twierdzeniem Weierstrassa dowolną funkcję y=f(x), ciągłą na przedziale domkniętym, można dowolnie przybliżyć za pomocą wielomianu odpowiednio wysokiego stopnia.

Metoda interpolacji polega na:

wybraniu n+1 punktów x0,x1,...,xn należących do dziedziny f, dla których znane są wartości

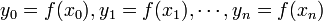
$y_0=f(x_0),y_1=f(x_1),\cdots ,y_n=f(x_n)$
znalezieniu wielomianu W(x) stopnia co najwyżej n takiego, że

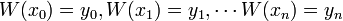
$W(x_0)=y_0,W(x_1)=y_1,\cdots W(x_n)=y_n$

Interpretacja geometryczna – dla danych n+1 punktów na wykresie szuka się wielomianu stopnia co najwyżej n, którego wykres przechodzi przez dane punkty.

Znajdowanie odpowiedniego wielomianu

Wielomian przyjmujący zadane wartości w konkretnych punktach można zbudować w ten sposób:

Dla pierwszego węzła o wartości f(x0) znajduje się wielomian, który w tym punkcie przyjmuje wartość f(x0), a w pozostałych węzłach x1,x2,...,xn wartość zero.
Dla kolejnego węzła znajduje się podobny wielomian, który w drugim węźle przyjmuje wartość f(x1), a w pozostałych węzłach x0,x2,...,xn wartość zero.
Dodaje się wartość ostatnio obliczonego wielomianu do wartości poprzedniego.
Dla każdego z pozostałych węzłów znajduje się podobny wielomian, za każdym razem dodając go do wielomianu wynikowego.
Wielomian będący sumą wielomianów obliczonych dla poszczególnych węzłów jest wielomianem interpolującym.

Dowód ostatniego punktu i dokładny sposób tworzenia poszczególnych wielomianów opisany jest poniżej w dowodzie istnienia wielomianu interpolującego będącego podstawą algorytmu odnajdowania tego wielomianu.

Wielomian Lagrange'a

Postać Lagrange'a wielomianu to jedna z metod przedstawiania wielomianu, wykorzystywana często w zagadnieniach interpolacji. Dla wielomianu stopnia n wybiera się n+1 punktów – x0,x1,...,xn i wielomian ma postać:

Ponieważ
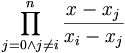$\prod_{j=0 \and j\ne i}^n \frac{x-x_j}{x_i-x_j}$ jest równy 1 dla x równego xi (licznik i mianownik są równe), 0 zaś dla wszystkich innych xj (licznik jest równy zero), można łatwo za pomocą postaci Lagrange'a interpolować dowolną funkcję:

$L_f(x) = \sum_{i=0}^n f(x_i) \prod_{j=0 \and j\ne i}^n \frac{x-x_j}{x_i-x_j}$

Wielomian ten będzie się zgadzał z funkcją f we wszystkich punktach xi.

Szybka transformacja Fouriera

Szybka transformacja Fouriera (ang. fast Fourier transform, FFT) – algorytm liczenia dyskretnej transformaty Fouriera oraz transformaty do niej odwrotnej.

Czasem używana jest też forma szybka transformata Fouriera w odniesieniu do tej metody. Ściśle jednak transformacja jest przekształceniem, a transformata wynikiem tego przekształcenia.

Niech x0, ...., xN-1 będą liczbami zespolonymi, wtedy dyskretna transformata Fouriera jest określona wzorem:

$X_k = \sum_{n=0}^{N-1} x_n e^{-{2\pi i \over N} nk } \qquad k = 0,\dots,N-1.$

Obliczanie tych sum za pomocą powyższego wzoru zajęłoby O(N2) operacji.

Algorytmy (jak algorytm Cooleya-Tukeya) obliczające szybką transformację Fouriera bazują na metodzie dziel i zwyciężaj, rekurencyjnie dzieląc transformatę wielkości N = N1N2 na transformaty wielkości N1 i N2 z wykorzystaniem O(N) operacji mnożenia.

Najpopularniejszą wersją FFT jest FFT o podstawie 2. Jest to bardzo efektywna operacja, jednak wektor próbek wejściowych (spróbkowany sygnał) musi mieć długość N=2^k, gdzie k to pewna liczba naturalna. Wynik otrzymuje się na drodze schematycznych przekształceń, opartych o tak zwane struktury motylkowe.

Złożoność obliczeniowa Szybkiej transformacji Fouriera wynosi O(N \log_2 N), zamiast O(N^2) algorytmu wynikającego wprost ze wzoru określającego dyskretną transformatę Fouriera. Dzięki istnieniu takiego algorytmu praktycznie możliwe stało się cyfrowe przetwarzanie sygnałów (DSP), a także zastosowanie dyskretnych transformat kosinusowych (DCT) (JPEG, MP3 itd.) do kompresji.

WAŻNE LINKI:

http://wazniak.mimuw.edu.pl/index.php?title=Metody_numeryczne

https://pl.wikipedia.org/wiki/Metoda_numeryczna

https://www.youtube.com/watch?v=uxu004QjtuU

https://www.youtube.com/watch?v=R-z1KXTXUWc

https://www.youtube.com/watch?v=N8fbW_B19ew

piątek, 9 października 2015

https://www.youtube.com/watch?v=e-luonb2VoM

METODY NUMERYCZNE Metoda Newtona Cotesa - WSB Radom Ohirko Ighor

https://pl.wikipedia.org/wiki/Metoda_numeryczna

http://wazniak.mimuw.edu.pl/index.php?title=Metody_numeryczne

https://www.youtube.com/watch?v=C7fPZtWKJ1Y