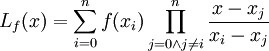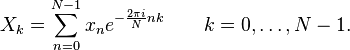Witam na moim blogu.
Będzie on poświęcony metodom numerycznym, a dokładnie wybranym zagadnieniom z tego działu.
Blog ten tworzony jest na potrzeby przedmiotu "Metody numeryczne". Prowadzącym jest profesor Ihor Ohirko (zdjęcie poniżej).
Co to są metody numeryczne?
Metody numeryczne to dziedzina wiedzy zajmująca się
problemami obliczeniowymi i konstrukcją algorytmów rozwiązywania zadań
matematycznych. Najczęściej, zadania obliczeniowe postawione są w dziedzinie
rzeczywistej (lub zespolonej) i dlatego mówimy o zadaniach obliczeniowych
matematyki ciągłej (w odróżnieniu od matematyki dyskretnej).
Metody numeryczne wykorzystywane są wówczas, gdy badany
problem nie ma w ogóle rozwiązania analitycznego (danego wzorami) lub
korzystanie z takich rozwiązań jest uciążliwe ze względu na ich złożoność.
W szczególności dotyczy to:
- całkowania;
- znajdowania miejsc zerowych wielomianów stopnia większego
niż 2 (korzystanie ze wzorów na dokładne wartości pierwiastków równań stopnia 3
i stopnia 4 jest niepraktyczne, dla równań stopnia wyższego niż 4 wzorów już
nie ma);
- rozwiązywania układów równań liniowych w przypadku większej
liczby równań i niewiadomych;
- rozwiązywania równań różniczkowych i układów takich równań;
- znajdowania wartości i wektorów własnych (zob. równanie
własne);
- aproksymacji, czyli przybliżaniu nieznanych funkcji (np.
pomiarów zjawisk fizycznych).
Niektóre metody numeryczne
- Interpolacja liniowa
- Interpolacja wielomianowa
- FFT
- metoda Monte Carlo
- metody Newtona-Cotesa
- wzór parabol Simpsona
- wzór trapezów
- metoda równego podziału
- Kwadratury Gaussa
Interpolacja liniowa – szczególny przypadek aproksymacji za pomocą funkcji liniowej.
Aproksymacja (łac. approximare – przybliżać) – proces określania rozwiązań przybliżonych na podstawie rozwiązań znanych, które są bliskie rozwiązaniom dokładnym w ściśle sprecyzowanym sensie. Zazwyczaj aproksymuje się byty (np. funkcje) skomplikowane bytami prostszymi. Często stosowana w przypadku szukania rozwiązań dla danych uzyskanych metodami empirycznymi, które mogą być obarczone błędami.
Jeśli x określa wartość z przedziału x0 < x < x1, a y0 = f(x0) i y1 = f(x1) tablicę wartości danej funkcji, oraz h = x1 - x0 odstęp pomiędzy argumentami, wówczas liniową interpolację wartości L(x) funkcji f otrzymuje się jako:
Interpolacja liniowa
Interpolacja wielomianowa, nazywana też interpolacją Lagrange'a, od nazwiska pioniera badań nad interpolacją Josepha Lagrange'a, lub po prostu interpolacją jest metodą numeryczną przybliżania funkcji tzw. wielomianem Lagrange'a stopnia n przyjmującym w n+1 punktach, zwanych węzłami interpolacji, wartości takie same jak przybliżana funkcja.
Interpolacja jest często stosowana w naukach doświadczalnych, gdzie dysponuje się zazwyczaj skończoną liczbą danych do określenia zależności między wielkościami.
Zgodnie z twierdzeniem Weierstrassa dowolną funkcję y=f(x), ciągłą na przedziale domkniętym, można dowolnie przybliżyć za pomocą wielomianu odpowiednio wysokiego stopnia.
Metoda interpolacji polega na:
- wybraniu n+1 punktów x0,x1,...,xn należących do dziedziny f,
dla których znane są wartości
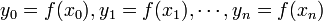
- znalezieniu wielomianu W(x) stopnia co najwyżej n takiego,
że
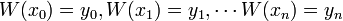
Interpretacja geometryczna – dla danych n+1 punktów na
wykresie szuka się wielomianu stopnia co najwyżej n, którego wykres przechodzi
przez dane punkty.
Znajdowanie odpowiedniego wielomianu
Wielomian przyjmujący zadane wartości w konkretnych punktach
można zbudować w ten sposób:
- Dla pierwszego węzła o wartości f(x0) znajduje się
wielomian, który w tym punkcie przyjmuje wartość f(x0), a w pozostałych węzłach
x1,x2,...,xn wartość zero.
- Dla kolejnego węzła znajduje się podobny wielomian, który w
drugim węźle przyjmuje wartość f(x1), a w pozostałych węzłach x0,x2,...,xn
wartość zero.
- Dodaje się wartość ostatnio obliczonego wielomianu do
wartości poprzedniego.
- Dla każdego z pozostałych węzłów znajduje się podobny
wielomian, za każdym razem dodając go do wielomianu wynikowego.
- Wielomian będący sumą wielomianów obliczonych dla
poszczególnych węzłów jest wielomianem interpolującym.
Dowód ostatniego punktu i dokładny sposób tworzenia
poszczególnych wielomianów opisany jest poniżej w dowodzie istnienia wielomianu
interpolującego będącego podstawą algorytmu odnajdowania tego wielomianu.
Wielomian Lagrange'a
Postać Lagrange'a wielomianu to jedna z metod przedstawiania
wielomianu, wykorzystywana często w zagadnieniach interpolacji. Dla wielomianu
stopnia n wybiera się n+1 punktów – x0,x1,...,xn i wielomian ma postać:
Ponieważ
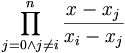
jest równy 1 dla x równego xi (licznik i mianownik są
równe), 0 zaś dla wszystkich innych xj (licznik jest równy zero), można łatwo
za pomocą postaci Lagrange'a interpolować dowolną funkcję:
Wielomian ten będzie się zgadzał z funkcją f we wszystkich
punktach xi.
Szybka transformacja Fouriera
Szybka transformacja Fouriera (ang. fast Fourier transform,
FFT) – algorytm liczenia dyskretnej transformaty Fouriera oraz transformaty do
niej odwrotnej.
Czasem używana jest też forma szybka transformata Fouriera w
odniesieniu do tej metody. Ściśle jednak transformacja jest przekształceniem, a
transformata wynikiem tego przekształcenia.
Niech x0, ...., xN-1 będą liczbami zespolonymi, wtedy
dyskretna transformata Fouriera jest określona wzorem:
Obliczanie tych sum za pomocą powyższego wzoru zajęłoby
O(N2) operacji.
Algorytmy (jak algorytm Cooleya-Tukeya) obliczające szybką
transformację Fouriera bazują na metodzie dziel i zwyciężaj, rekurencyjnie
dzieląc transformatę wielkości N = N1N2 na transformaty wielkości N1 i N2 z
wykorzystaniem O(N) operacji mnożenia.
Najpopularniejszą wersją FFT jest FFT o podstawie 2. Jest to
bardzo efektywna operacja, jednak wektor próbek wejściowych (spróbkowany
sygnał) musi mieć długość N=2^k, gdzie k to pewna liczba naturalna. Wynik
otrzymuje się na drodze schematycznych przekształceń, opartych o tak zwane
struktury motylkowe.
Złożoność obliczeniowa Szybkiej transformacji Fouriera
wynosi O(N \log_2 N), zamiast O(N^2) algorytmu wynikającego wprost ze wzoru
określającego dyskretną transformatę Fouriera. Dzięki istnieniu takiego
algorytmu praktycznie możliwe stało się cyfrowe przetwarzanie sygnałów (DSP), a
także zastosowanie dyskretnych transformat kosinusowych (DCT) (JPEG, MP3 itd.)
do kompresji.
WAŻNE LINKI:
http://wazniak.mimuw.edu.pl/index.php?title=Metody_numeryczne
https://pl.wikipedia.org/wiki/Metoda_numeryczna
https://www.youtube.com/watch?v=uxu004QjtuU
https://www.youtube.com/watch?v=R-z1KXTXUWc
https://www.youtube.com/watch?v=N8fbW_B19ew





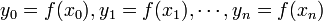
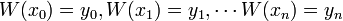

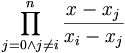 jest równy 1 dla x równego xi (licznik i mianownik są
równe), 0 zaś dla wszystkich innych xj (licznik jest równy zero), można łatwo
za pomocą postaci Lagrange'a interpolować dowolną funkcję:
jest równy 1 dla x równego xi (licznik i mianownik są
równe), 0 zaś dla wszystkich innych xj (licznik jest równy zero), można łatwo
za pomocą postaci Lagrange'a interpolować dowolną funkcję: